Pelajaran matematika tentang sifat pangkat bilangan bulat
pengertian kuadrat suatu bilangan. Kuadrat atau pangkat dua suatu bilangan adalah mengalikan suatu bilangan dengan bilangan itu sendiri. Lebih lanjut, perpangkatan suatu bilangan artinya perkalian berulang dengan bilangan yang sama. Perhatikan perpangkatan bilangan pokok 2 berikut.
21 = 2
22 = 2 x 2 (22 dibaca 2 kuadrat atau 2 pangkat 2) = 4
23 = 2 x 2 x 2 (23 dibaca 2 pangkat 3) = 8
2n = 2 x 2 x 2 x . . . 2 (2n dibaca 2 pangkat n)
Pn = p x p x p x . . . p (p dikalikan sebanyak n faktor)
Dengan p disebut bilangan pokok dan n disebut pangkat (eksponen). Untuk p 0 maka p0 = 1 dan p1 = p
0 maka p0 = 1 dan p1 = p
Untuk memperjelas materi ini, coba kamu perhatikan contoh berikut!
a. 92
b. (-6)3
c. (-10)4
Pembahasan.
a. 92 = 9 x 9
92 = 81
b. (-6)3 = -6 x -6 x -6
= 36 x -6
= - 48
b. (-10)3 = -10 x -10 x -10 x -10
= 100 x 100
= 10.000
Coba perhatikan, bilangan bulat negatif jika berpangkat ganjil maka menghasilkan bilangan bulat negatif, dan sebaliknya jika pangkatnya genap maka menghasilkan bilangan bulat positif.

Jika m, n bilangan bulat positif dan p bilangan bulat maka :
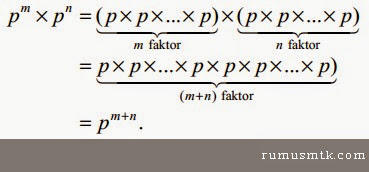

Jika m, n bilangan bulat positif dan p bilangan bulat maka :


Jika m, n bilangan bulat positif dan p bilangan bulat maka :

(5 x 2)3 = 103 = 1.000
(5 x 2)3 = 53 x 23 = 125 x 8 = 1.000
Berdasarkan uraian di atas, dapat kita tuliskan sebagai berikut. Jika m bilangan bulat positif dan p, q bilangan bulat maka
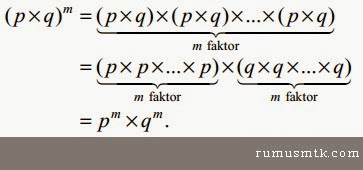
Sifat perpangkatan pada bilangan bulat yang ke (iv) juga berlaku untuk pembagian. Coba kamu diskusikan dengan teman sekelas, buktikan sendiri bahwa :
(p : q)m = pm: pm
21 = 2
22 = 2 x 2 (22 dibaca 2 kuadrat atau 2 pangkat 2) = 4
23 = 2 x 2 x 2 (23 dibaca 2 pangkat 3) = 8
2n = 2 x 2 x 2 x . . . 2 (2n dibaca 2 pangkat n)
Secara umum dapat dituliskan sebagai berikut. Untuk sebarang bilangan bulat p dan bilangan bulat positif n,
berlaku :Pn = p x p x p x . . . p (p dikalikan sebanyak n faktor)
Dengan p disebut bilangan pokok dan n disebut pangkat (eksponen). Untuk p
Untuk memperjelas materi ini, coba kamu perhatikan contoh berikut!
a. 92
b. (-6)3
c. (-10)4
Pembahasan.
a. 92 = 9 x 9
92 = 81
b. (-6)3 = -6 x -6 x -6
= 36 x -6
= - 48
b. (-10)3 = -10 x -10 x -10 x -10
= 100 x 100
= 10.000
Coba perhatikan, bilangan bulat negatif jika berpangkat ganjil maka menghasilkan bilangan bulat negatif, dan sebaliknya jika pangkatnya genap maka menghasilkan bilangan bulat positif.
Sifat-sifat perpangkatan pada bilangan bulat
(i) Sifat perkalian bilangan berpangkat
Perhatikan perkalian bilangan bulat berpangkat berikut.
Jika m, n bilangan bulat positif dan p bilangan bulat maka :
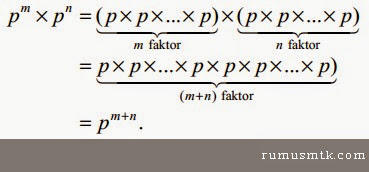
(ii). Sifat pembagian bilangan berpangkat
Perhatikan pembagian bilangan bulat berpangkat berikut.
Jika m, n bilangan bulat positif dan p bilangan bulat maka :

(iii). Sifat perpangkatan bilangan berpangkat

Jika m, n bilangan bulat positif dan p bilangan bulat maka :

(iv). Sifat perpangkatan suatu perkalian atau pembagian
Perhatikan contoh soal berikut ini,(5 x 2)3 = 103 = 1.000
(5 x 2)3 = 53 x 23 = 125 x 8 = 1.000
Berdasarkan uraian di atas, dapat kita tuliskan sebagai berikut. Jika m bilangan bulat positif dan p, q bilangan bulat maka
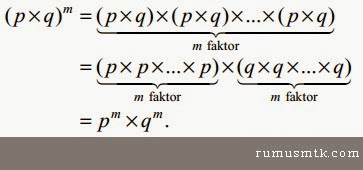
Sifat perpangkatan pada bilangan bulat yang ke (iv) juga berlaku untuk pembagian. Coba kamu diskusikan dengan teman sekelas, buktikan sendiri bahwa :
(p : q)m = pm: pm
Kesimpulan
(a) pm x pn= pm+n
(b) pm : pn= pm-n
(c) (pm)n= pm x n
(d) (p x q)m = pmx pm
(e) (p : q)m = pm: pm
Dengan catatan p dan q disebut bilangan pokok sedangkan m dan n bilangan pangkat (eksponen), semuanya merupakan bilangan bulat.
(a) pm x pn= pm+n
(b) pm : pn= pm-n
(c) (pm)n= pm x n
(d) (p x q)m = pmx pm
(e) (p : q)m = pm: pm
