CONTOH POLA PENGUBINAN KELAS 1 SD
Rifanfajrin.com - CONTOH POLA PENGUBINAN KELAS 1 SD
Pengubinan
ialah prosedur penempatan bangun datar dalam suatu luasan secara tepat tanpa
celah. Aturan penempatan bangun datar dalam menutupi sebuah luasan bertujuan menghasilkan
sebuah karya seni yang masih menggunakan prinsip-prinsip matematika.
Pengubinan berkembang pada zaman Romawi Kuno, dan merupakan Karya Seni dalam kebudayaan
Muslim.
Kata
tessellation pengubinan merupakan bahasa Yunani tessera, berkaitan dengan segiempat
dan ubin. Inilah alasannya mengapa ubin bentuk segiempat. Segiempat sendiri
adalah bangun yang yang paling mudah dipasang
tanpa menyisahkan celah.
Ubin
adalah bahan seni dekoratif yang ada disekeliling kita. Terdapat dua orang yang
mengembangkan pengubinan, yaitu Roger
Penrose, seorang ahli matematika terkemuka, dan seniman, M.C.Escher.
Materi
tentang pengubinan memungkinkan anak-anak untuk menghasilkan karya seni dalam
berbagai mata pelajaran, seperti prakarya, matematika dan IPS (sejarah).
Pengubinan
adalah konsep matematika penting yang diberikan kepada siswa SD sejak kelas 1.
Oleh sebab itu, penting bagi guu untuk memahami konsep pengubinan tersebut agar dapat mengajarkan
konsep pengubinan pada siswa sekolah dasar dengan baik dan benar.
1. Pengertian Pengubinan
Daerah
segibanyak adalah gabungan antara segibanyak dan daerah didalamnya. Penyusunan
daerah-daerah segibanyak yang sisi-sisinya berimpit sehingga menutup bidang
secara sempurna tidakadabagianyangtidaktertutup dinamakan pengubinan.
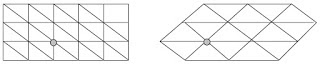
Gambar-gambar berikut ini menunjukkan pengubinan dengan segitiga-segitiga
siku-siku dan pengubinan dengan segitiga sama kaki.
2. Pengubinan dengan berbagai segibanyak
Perhatikan
kedua gambar di atas. Pada gambar pertama menunjukkan pengubinan dengan
segitiga siku-siku. Pola pada pengubinan ini adalah ada 6 segitiga siku-siku
bertemu pada satu titik. Keadaan seperti ini dikatakan bahwa konfigurasi
segitiga siku-siku bertemu di satu titik adalah 3,3,3,3,3,3.
Barisan enam 3-an ini menyatakan bahwa ada enam segitiga siku-siku bertemu pada setiap titik sudutnya. Hal serupa juga terjadi pada gambar kedua. Pada gambar kedua, konfigurasi segitiga sama kaki bertemu di satu titik adalah juga 3,3,3,3,3,3.
Mintalah
siswa bekerja dalam kelompok membuat pengubinan dengan menggunakan segitiga
sama sisi, persegipanjang, trapesium, dan layang-layang. Kemudian mintalah
mereka menuliskan konfigurasinya.
Perhatikan gambar sebuah bangun segienam beraturan di atas. Jika kita akan melihat apakah mungkin kita dapat melakukan pengubinan dengan bangun-bangun segienam itu dan bagaimana bentuk konfigurasi segienam beraturan itu bertemu pada satu titik, maka harus memusatkan perhatian pada salah satu sudut segi enam beraturan itu. Untuk itu perhatikan lingkaran yang ada pada salah satu sudut segienam beraturan di atas. Misalkan kita telah mengetahui bahwa besar satu sudut segi enam beraturan adalah 120 dan kita telah mengetahui bahwa besar sudut satu lingkaran penuh adalah 360. Kita ingin mengetahui apakah mungkin ada beberapa segienam beraturan lain yang dapat menutup daerah lingkaran yang tersisa. Karena kita sudah mempunyai sudut sebesar 120, kita masih memerlukan gabungan sudut dari beberapa segienam beraturan yang besarnya adalah 360 – 120 = 240. Karena itu kita memerlukan dua buah bangun segienam lagi. Dengan demikian, konfigurasi pengubinan dengan menggunakan segienam beraturan bertemu pada sebuah titik adalah 6,6,6.
Pertanyaan selanjutnya adalah, apakah mungkin kita membuat pengubinan menggunakan hanya bangun-bangun segilima beraturan? Misalkan kita telah mengetahui bahwa besar satu sudut segi lima beraturan adalah 1080. Untuk itu kita masih memerlukan gabungan sudut-sudut dari beberapa segilima beraturan yang besarnya 360 – 108 = 252. Ada berapa buah sudut segilima beraturan sehingga berukuran 2520? Karena satu sudut segilima beraturan besarnya 1080, kita tidak memperoleh bilangan bulat yang menyatakan banyaknya sudut segilima yang diperlukan. Dengan demikian, kita tidak dapat melakukan pengubinan dengan menggunakan hanya bangun-bangun segilima dan gambarnya kira-kira seperti tampak berikut ini.
Untuk
menentukan pengubinan bangun-bangun segibanyak beraturan, kita harus memahami
besar setiap sudut pada segibanyak beraturan. Kita telah mengetahui bahwa
jumlah ukuran sudut segitiga adalah 180 dan besar ukuran sudut satu lingkaran
penuh adalah 360. Meskipun demikian, mungkin banyak diantara kita belum
mengetahui besar ukuran setiap sudut dalam segibanyak beratuarn. Untuk itu,
sebelum mengakhiri pembahasan pengubinan, kita bicarakan sedikit tentang besar
ukuran setiap sudut pada segibanyak beraturan, yaitu sebagai berikut:
1. Segitiga beraturan segitigasamasisi
Karena jumlah ukuran sudut dalam segitiga
beraturan adalah 180, besar ukuran setiap sudutnya adalah 60.
2. Segiempat beraturan persegi
Karena segiempat beraturan dapat
dibangun dari dua segitiga, maka jumlah ukuran sudut dalam segiempat itu adalah
2 x 180 = 360 lihatgambardibawahini. Dengan demikian, besar ukururan setiap
sudutnya adalah 90.
3. Segilima beraturan
Perhatikan
gambar berikut ini.
Gambar di atas
adalah segilima beraturan yang dibagi menjadi lima buah segitiga kongruen. Setiap
segitiga itu mempunyai jumlah ukuran sudut 1800, akibatnya, lima buah segitiga
mempunyai jumlah ukuran sudut 5 x 180 = 900. Ukuran sudut ini menunjukkan
gabungan antara jumlah ukuran segilima beraturan dan besar sudut pusatnya
sudutyangadaditengah−tengahsegilima. Karena ukuran sudut pusat itu adalah 360,
jumlah ukuran segilima beraturan itu adalah 900 – 360 = 540. Dengan demikian,
besar setiap sudut dalam segilima beraturan adalah 540 : 5 = 108.
4. Segienam
beraturan
Perhatikan gambar berikut ini.
Gambar di atas
adalah segienam beraturan yang dibagi menjadi enam buah segitiga kongruen.
Setiap segitiga itu mempunyai jumlah ukuran sudut 1800, akibatnya, enam buah
segitiga mempunyai jumlah ukuran sudut 6 x 1800 = 10800. Ukuran sudut ini
menunjukkan gabungan antara jumlah ukuran segilima beraturan dan besar sudut
pusatnya sudutyangadaditengah−tengahsegilima. Karena ukuran sudut pusat itu
adalah 360, jumlah ukuran segienam beraturan itu adalah 1080 – 360 = 720.
Dengan demikian, besar setiap sudut dalam segilima beraturan adalah 720 : 60 =
120.
Dari hasil nomor 1 sampai dengan nomor 4 di atas, kita dapan memperoleh pola untuk mencari besar steiap sudut segibanyak beraturan. Pola itu adalah sebagai berikut: